|
نظریه گراف و سؤالات حل شده |
با
عرض سلام به شما کاربر گرامی .... سؤالاتی که در زیر مشاهده میکنید
مربوط به تمرینات کلاسی درس نظریه گراف استاد
محترم جناب آقای زارع فرد میباشد.
لطفا
برای ادامه فعالیت در این زمینه نظرات و پیشنهادات خود را بیان
کنید.

سؤال 1
: بنا بر قضیه بالا نشان دهید تعداد رئوس فرد یک گراف زوج است.
************
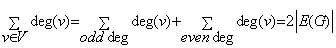


سؤال 2) می توان نشان داد که
هر مسیر حتما گذر است ولی عکس آن برقرار نیست .
برای عکس مطلب فوق یک مثال بیاورید .
************
گذری
که مسیر نیست.


سؤال 3) گراف G را دو بخشی
گویند اگر و فقط اگر دارای دوری به طول فرد نباشد .
عکس قضیه فوق را اثبات کنید
.
************
اگر G همبند باشد، و دور فرد نداشته باشد، a را یک
رأس دلخواه از گراف G در نظر میگیریم و قرار می دهیم :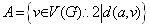 و
و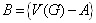 در این صورت
در این صورت
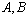 مجموعه
مجموعه
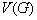 را افراز میکنند .ادعا می کنیم
را افراز میکنند .ادعا می کنیم
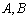 مجموعه های مستقل هستند، اگر
مجموعه های مستقل هستند، اگر
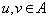 در این صورت طبق تعریف
در این صورت طبق تعریف
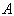 ، مسیر های
، مسیر های
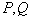 به طول زوج وجود دارند که
به طول زوج وجود دارند که
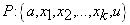 و
و
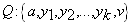
حال اگر
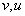 باشند آنگاه طول گشت بسته
باشند آنگاه طول گشت بسته
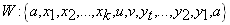 فرد است و لذا دارای دوری به طول فرد می باشد که با فرض در تناقض
است. بنابراین هیچکام از رئوس مجموعه
فرد است و لذا دارای دوری به طول فرد می باشد که با فرض در تناقض
است. بنابراین هیچکام از رئوس مجموعه
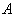 با
هم در ارتباط نیستند . همینطور ثابت می شود که اعضای مجموعه با
هم در ارتباط نیستند . همینطور ثابت می شود که اعضای مجموعه
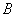 نیز با همدیگر رابطه ندارند . در نتیجه گراف
نیز با همدیگر رابطه ندارند . در نتیجه گراف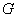 دوبخشی است.
دوبخشی است.


سؤال 4) فرض کنید که G یک گراف
r-منتظم باشد ، رابطه ای برای
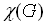 پیدا کنید.
پیدا کنید.
؟


سوال 5) ثابت کنید اگر G یک
گراف مسطح باشد و محیط آن 5 باشد در اینصورت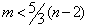
(توجه: منظور از محیط طول
کوتاهترین دور G است .)
************
اثبات: مجموعه S را
شامل همه زوج مرتب های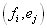 میگیریم
. این بدین معناست که مثلاً داریم که میگیریم
. این بدین معناست که مثلاً داریم که
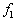 وجه اول است
، حال چون تعداد وجوه گراف وجه اول است
، حال چون تعداد وجوه گراف
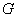 ، ،
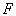 تا است و هر
وجه حداقل 5 یال دارد ، بنابراین مجموعه S حداقل شامل تا است و هر
وجه حداقل 5 یال دارد ، بنابراین مجموعه S حداقل شامل
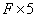 عضو است.و عضو است.و
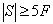 از طرفی چون داشتیم هر یال حداکثر متعلق به دو وجه است پس
از طرفی چون داشتیم هر یال حداکثر متعلق به دو وجه است پس
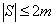 است
.بنابراین داریم : است
.بنابراین داریم :
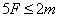 و طبق فرمول اویلر داریم :
و طبق فرمول اویلر داریم :
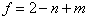 در نتیجه :
در نتیجه :
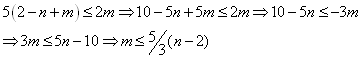


سؤال 6) اگر کمترین وجه G
را با
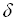 و بیشترین آنرا با
و بیشترین آنرا با
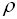 نمایش دهیم ، نشان دهید:
نمایش دهیم ، نشان دهید:
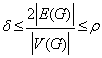
************
میدانیم که
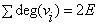 اما از
طرفی چون اما از
طرفی چون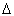 بزرگترین درجه
رئوس گراف میباشد داریم: بزرگترین درجه
رئوس گراف میباشد داریم: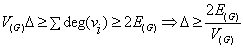
همینطور برای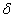 چون
چون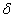 کوچکترین درجه رئوس
گراف میباشد داریم : کوچکترین درجه رئوس
گراف میباشد داریم :
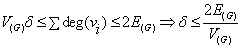
که از این دو تساوی داریم:
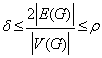


سؤال 7) اگر هرجفت از گزاره های
زیر رخ دهد ثابت کنید سومی رخ خواهد داد.:
1) G همبند است .
2) G فاقد دور است. 3)
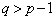
************
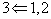 با توجه به تعریف درخت داریم که گراف همبند فاقد دور یک درخت است .
حال ثابت می کنیم که
با توجه به تعریف درخت داریم که گراف همبند فاقد دور یک درخت است .
حال ثابت می کنیم که
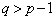 استقرا : با استقرا بر روی v ثابت می کنیم.
استقرا : با استقرا بر روی v ثابت می کنیم.
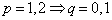
فرض می کنیم که حکم برای هر درخت با k رأس درست
باشد . یعنی
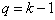
حال درخت با k+1 رأس را در نظر گرفته و با
توجه به اینکه هر درخت حداقل دو رأس از درجه یک دارد اگر از این
درخت یک رأس از درجه یک و یال مربوط به آن را حذف کنیم ، درختی
پدید می آید با k رأس و طبق فرض استقرا دارای k-1 یال . پس درخت
k+1 رأسی دارای k یال است . بدین ترتیب حکم ثابت شد.
************
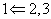 برهان خلف :
برهان خلف :
اگر گراف با مشخصات 2 و3
همبند نباشد ، بنابراین ناهمبند خواهد بود و دارای مؤلفه های
همبندی که چون دارای دور نیست هر مؤلفه همبندی یک درخت خواهد بود .
که برای هر مؤلفه داریم :
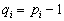 بنابراین :
بنابراین :
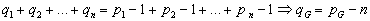
که در آن n تعداد مؤلفه های همبندی است . و
طبق فرض 3 داشتیم :
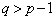 بنابراین داریم : n=1 در نتیجه G همبند است و بنابراین حکم ثابت
است .
بنابراین داریم : n=1 در نتیجه G همبند است و بنابراین حکم ثابت
است .
************
 برهان خلف : برهان خلف :
فرض می کنیم
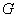 دور داشته باشد بناباین یال e را که در دور واقع است حذف می کنیم .
در اینصورت
دور داشته باشد بناباین یال e را که در دور واقع است حذف می کنیم .
در اینصورت
 همبند است .اگر
همبند است .اگر
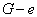 دور
داشته باشد باز هم یالی را حذف می کنیم تا گراف دور
داشته باشد باز هم یالی را حذف می کنیم تا گراف 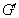 بدون دور بدست آید .
بدون دور بدست آید .
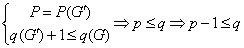
که تناقض است .

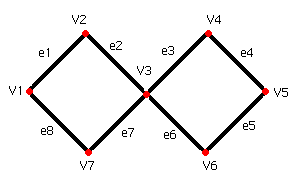
 سؤال 8)در
گراف زیر به کمک الگوریتم فلوری یک مدار اویلری برست آورید.
سؤال 8)در
گراف زیر به کمک الگوریتم فلوری یک مدار اویلری برست آورید.
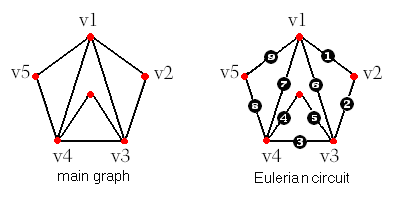


سؤال 9) فرض کنید G گراف
همبند باشد ، در هر یک از موارد زیر چه می توان گفت.
1) یالی که در هر درخت پوشای G ظاهر شود.
2) یالی که در هیچ درخت پوشای G ظاهر نشود.
************
در مورد اول چنین یالی یال برشی
خواهد بود که باید مطمئناً در گراف فراگیر باشد چون در صورت حذف
گراف ناهمبند خواهد شد.
در مورد دوم، چنین یالی وجود ندارد ، (برهان خلف) فرض می کنیم e
چنین یالی باشد ، در این صورت دو حالت وجود دارد . اول اینکه e در
هیچ دوری واقع نباشد لذا این یال یال برشی خواهد بود و امکان حذف
آن وجود ندارد . دوم اینکه این یال در دوری واقع باشد . بنابر این
با حذف یالی از دور به جزe میتوان درخت فراگیری تشکیل داد که شامل
e باشد.بنابراین در هر صورت میتوان از e در تشکیل درخت فراگیر
استفاده کرد .


سؤال 10)
نشان دهید که هر درخت حداکثر دو رأس مرکزی دارد.
************
جواب :با استقرا بر روی v ثابت می
کنیم . برای درخت با یک رأس یک مرکز و برای درخت با دو رأس دو مرکز
وجود دارد .
حال فرض می کنیم برای هر درخت T با کمتر یا مساوی k رأس حکم برقرار
باشد . حال درخت
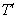 را با k+1
رأس را در نظر می گیریم ، ثابت میکنیم که را با k+1
رأس را در نظر می گیریم ، ثابت میکنیم که
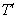 حداکثر یک یا
دو مرکز دارد . برای این کار ابتدا تمام رأس های درجه یک گراف را
حذف می کنیم . (چون هر درخت دارای حداقل دو رأس از درجه یک است )
درخت باقی مانده دارای حداکثر k-1 رأس است . که طبق فرض استقرا
دارای حداکثر دو مرکز است .واضح است که گریز از مرکز هررأس فاصله
آن از یک رأس درجه یک است . و نیز می دانیم که با اضافه کردن رئوس
درجه یک ، به گریز از مرکز همه رئوس یک و فقط یک واحد افزوده می
شود . بنابراین با اضافه کردن رئوس درجه یک به درخت k-1 رأسی مراکز
درخت حداکثر یک یا
دو مرکز دارد . برای این کار ابتدا تمام رأس های درجه یک گراف را
حذف می کنیم . (چون هر درخت دارای حداقل دو رأس از درجه یک است )
درخت باقی مانده دارای حداکثر k-1 رأس است . که طبق فرض استقرا
دارای حداکثر دو مرکز است .واضح است که گریز از مرکز هررأس فاصله
آن از یک رأس درجه یک است . و نیز می دانیم که با اضافه کردن رئوس
درجه یک ، به گریز از مرکز همه رئوس یک و فقط یک واحد افزوده می
شود . بنابراین با اضافه کردن رئوس درجه یک به درخت k-1 رأسی مراکز
درخت
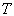 همان مراکز درخت
همان مراکز درخت
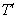 میباشد.
میباشد.


سؤال11)
نشان دهید اگر G گرافی k-منتظم باشد L(G) گرافی 2k-2-منتظم خواهد
بود.
************
چون هر یال در گراف G یک رأس در گراف L(G)
است و هر یال به دو رأس از دو سر منتهی میشود، و همچنین چون درجه
هر رأسG ، k است پس یال e از هر سر با k-1 یال دیگر در ارتباط است،
بنابراین یال دلخواه e که در L(G) رأس e خواهد بود با
(k-1+k-1)=2k-2 رأس دیگر در ارتباط است.


سوال 12) : هر گراف مسطح ماکزیمال
یک گراف مثلثی است .
************
برهان : (برهان خلف) فرض کنید
گرافG مسطح ماکزیمال باشد اما مثلثی نباشد یعنی حداقل یک وجه آن
دارای بیشتر از 3 یال باشد، که در این صورت میتوان با رسم یکی از
اقطار این وجه گرافی مسطح بدست آورد که این با فرض مسطح ماکزیمال
بودن G متناقض است.


سؤال 13)اگر گراف مسطح ماکزیمال
باشد در اینصورت
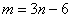 که n تعداد رئوس و m تعداد یال
های G است . که n تعداد رئوس و m تعداد یال
های G است .
************
برهان : با توجه به اینکه هر گراف
مسطح ماکزیمال ، مثلثی است . داریم :
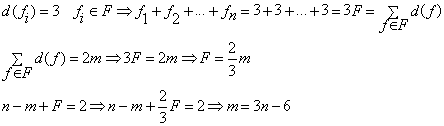


با سلام به همه دوستان عزیز مخصوصا آقای اصفهانی
که در قسمت نظرات سوال 10 گفته بودند سوال باید به صورت زیر باشه:
نشان دهید که هر درخت حداقل
دو رأس مرکزی دارد.
اما من فکر میکنم
حداکثر درسته ،
چون یک مرجع معتبر لاتین این طور بیان کرده بود من هم صلاح دونستم
سؤال رو به این صورت بنویسم.
شاید شما رأس مرکزی رو با رأس درجه یک اشتباه
گرفتید!؟!؟
من قسمت هایی از اون مرجع رو
مینویسم .
ضمنا شما اگه یک درخت با یک رأس رو
در نظر بگیرید بدیهیست که این درخت یک رأس درجه یک داره پس
مثال نقضی واسه چیزی که شما میگید هست !!!
The distance dG(u, v)
between two (not necessary distinct) vertices u and v in a graph
G is the length of a shortest path between them. The subscript G
is usually dropped when there is no danger of confusion. When u
and v are identical, their distance is 0. When u and v are
unreachable from each other, their distance is defined to be
infinity ∞.
The eccentricity εG(v) of a vertex v in a graph G is the maximum
distance from v to any other vertex. The diameter diam(G) of a
graph G is the maximum eccentricity over all vertices in a
graph; and the radius rad(G), the minimum. When there are two
components in G, diam(G) and rad(G) defined to be infinity ∞.
Trivially, diam(G) ≤ 2 rad(G). Vertices with maximum
eccentricity are called peripheral vertex. Vertices of minimum
eccentricity form the center. A tree
has at most two center vertices.
************
WWW.WIKIPEDIA.COM

سؤال14 )
ثابت کنید اگر گرافی ساده دارای دقیقاَ 2n+1 رأس
باشد و نیز تعداد یال های G بیشتر از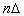 باشد آنگاه :
باشد آنگاه :
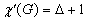
؟


سؤال 15) عبارتی برای تعداد یالهای
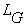 بر اساس درجات رئوس G بیابید.
بر اساس درجات رئوس G بیابید.
************
با توجه به شکل مشاهده می شود به ازای هر رأس
با درجه n تعداد
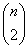 یال در یال در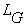 خواهیم
داشت . خواهیم
داشت .
حال تعداد کل یالها
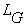 از فرمول زیر بدست می آید که در آن
از فرمول زیر بدست می آید که در آن
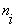 درجه
رأس iام است درجه
رأس iام است
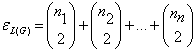


Comming Soon
Comming Soon
جدید:
جزوه کامل
آموزش نظریه گراف به زودی
|